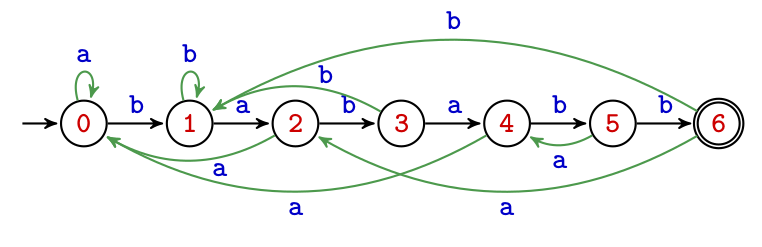
On considère l'automate fini déterministe A qui reconnait tous les mots sur l'alphabet {a,b} qui ne contiennent pas de b isolé.
Cet automate
{a,b}{0,1,2,3}0 est l'état initial0 et 2 sont les états d'acceptation| a | b | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 3 | 2 |
| 2 | 0 | 2 |
| 3 | 3 | 3 |
Pour sa mise en oeuvre en Java, on utilise la classe Automate et un programme de test TestAutomate
import java.util.*; public class Automate { /** La fonction de transition de l'automate */ protected int[][] _tableTransitions; /** État initial */ protected int _etatInitial; /** Liste d’états finaux */ protected List<Integer> _etatsFinaux; public Automate(int Initial, Integer[] Acceptants, int[][] _tableTransitions) { this._tableTransitions = _tableTransitions; this._etatInitial = Initial; this._etatsFinaux = Arrays.asList(Acceptants); } /** État interne de l'automate */ protected int etat; /** Positionne l'automate dans son état initial */ protected void etatInitial() { etat = _etatInitial; } /** L'état courant est-il acceptant ? */ protected boolean etatCourantEstAcceptant() { return _etatsFinaux.contains(etat); } /** Étant donné un caractère (donné par son code unicode), déclencher la transition */ protected void etatSuivant(char c) { etat = _tableTransitions[etat][c-'a']; } public boolean reconnait(String mot) { etatInitial(); char[] ch = mot.toCharArray(); for (int i = 0; i < mot.length(); i++) { char c=ch[i]; System.out.println("État : "+ etat + " entrée " + String.format("%c", c)); etatSuivant(c); } System.out.println("État : "+ etat); return etatCourantEstAcceptant(); } }
Apublic class TestAutomate { static Automate automate = new Automate( 0, new Integer[] {0,2}, new int[][] {{0,1}, {3,2}, {0,2}, {3,3}} ); public static void main(String args[]) { if (args.length < 1) { System.err.println("Usage : TestAutomate mots ..."); System.exit(1); } for (int i = 0; i < args.length; i++) { String arg = args[i]; boolean r = automate.reconnait(arg); System.out.println("\"" + arg + "\"" + (r ? " est" : " n'est pas") + " reconnu\n"); } } }
A sur diverses entrées : abbabb, ababbb, abbabbaaab, aaaa ... 6 qui ne soit pas reconnus par A
et deux mots de longueur 6 qui soit reconnus.
À présent, on s'intéresse au problème de recherche de motif dans un texte.
Il s'agit de retrouver toutes les occurrences d’un mot u dans un texte t.
On envisage deux algorithmes de recherche basés sur des automates finis.
Σ*u -- l'ensemble des mots sur Σ qui se terminent par u --t avec cet automate :
l'automate lit le texte t, caractère par caractère; il détecte une occurrence du mot u à chaque fois qu'il entre dans un état d'acceptation.bababb
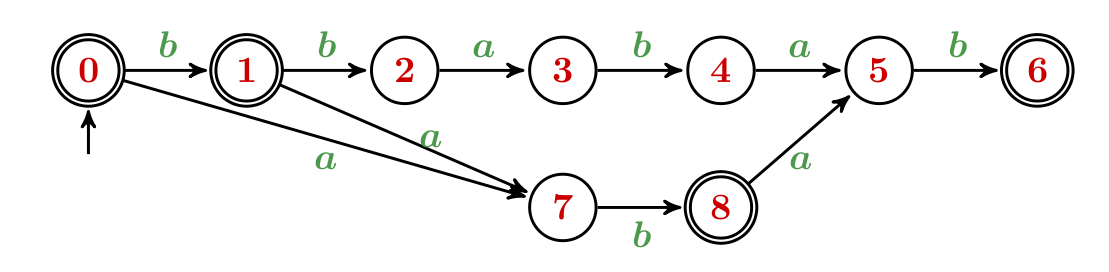
L'AFD qui reconnaît {a,b}*bababb est décrit par le graphe de transition suivant :

TestAutomate_bababb pour tester cet automate sur les entrées bababb, babbababb (on s'inspirera de la classe TestAutomate).t=bbabaabababbababbaba.bababb dans le texte t ?compte qui prend en entrée un texte t et affiche le nombre d'occurences du mot bababb dans le texte t.Remarque.
L'automate entre dans l'état i quand le plus long suffixe de la partie actuellement lue de t qui est préfixe de u est de longueur i.
u quelconque, construire un AFD qui reconnaît Σ*u
Soit m la longueur du motif u, l'AFD qui reconnaît Σ*u se calcule comme suit :
m+1 états {0,1,..,m}0{m}δ:{0,1,..,m}* Σ → {0,1,..,m} où δ(i,a) est définie comme le nombre de lettres du plus grand suffixe u[:i]a qui soit aussi préfixe de u.δ(i,a) =
i+1 si a=u[i] (arc avant)max{j≤ i: u[:j]=u[i-j+1:i]a} sinon (arc arrière)v et qui détermine la taille du plus grand suffixe de v qui soit aussi préfixe du motif u. AutomateLoc et écrire le constructeur qui prend le motif u en argument et construit l'AFD Σ*u.analyser qui prend en entrée un texte t et qui signale la position de toutes les ocurences du mot u dans tu et textes t.Référence. C. Charras - T. Lecroq : Deterministic Finite Automaton algorithm
On utilise une fenêtre coulisante de la taille du mot u cherché qui se déplace le long du texte.
Initialement cette fenêtre est au début du texte.
Quand la fenêtre est positionnée en i,
on détermine le plus long préfixe pref de u qui soit suffixe du texte inscrit dans la fenêtre.
pref est plus petit que u, on décale la fenêtre au début de pref (toutes les positions précédentes sont vouées à l'échec);
pref est u lui même, une occurrence est détectée et on décale la fenêtre au début du précédent préfixe rencontré.
| pref | |||||||||||||||||||||||||||
| Le texte | b | a | b | b | a | b | a | a | b | a | b | a | b | b | a | a | a | b | a | b | a | b | b | b | a | b | a |
| Fenêtre de | i | à | i+|u|-1 | ||||||||||||||||||||||||
Comment déterminer ce préfixe de u qui soit le plus long
suffixe de la fenêtre lue ?
En cherchant de droite à gauche dans la fenêtre (i.e dans le sens inverse)
les suffixes du mot miroir de u (i.e. le mot lu en sens
inverse).
Concrétement, on construit l'automate des suffixes du mot miroir de u
(l'AFD qui reconnaît tous les suffixes du mot miroir).
On applique l'automate sur les caractères de la fenêtre lue de
droite à gauche, et à chaque fois que l'automate entre dans un état
final (sans que tous les caractères de la fenêtre n'aient été consommés)
on mémorise la position dans une variable der.
bababbbbabab.
babbabaabababbaaabababbbaba.
La fenêtre est de longueur m = |bababb| = 6. On déroule l'automate avec
comme entrée le dernier caractère de la fenêtre, ici b qui fait passer
l'automate à l'état 1 ; 1 étant final, on mémorise der = 1. Puis
l'entrée a pour l'état 7 qui n'est pas final. Et b
pour l'état 8 qui est final, donc der = 3. Le b
suivant fait passer l'automate dans un état puits et on peut arrêter la
reconnaissance.
| Le texte | b | a | b | b | a | b | a | a | b | a | b | a | b | b | a | a | a | b | a | b | a | b | b | b | a | b | a |
| États | ⊥ | 8 | 7 | 1 | 0 |
m - der, soit 3 caractères,
et on recommence.
| Le texte | b | a | b | b | a | b | a | a | b | a | b | a | b | b | a | a | a | b | a | b | a | b | b | b | a | b | a |
| États | ⊥ | 7 | 1 | 0 |
der vaut 1, on décale la fenêtre de 5.
| Le texte | b | a | b | b | a | b | a | a | b | a | b | a | b | b | a | a | a | b | a | b | a | b | b | b | a | b | a |
| États | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
bababb est trouvé, et comme der vaut 1, on décale la fenêtre de 5.
| Le texte | b | a | b | b | a | b | a | a | b | a | b | a | b | b | a | a | a | b | a | b | a | b | b | b | a | b | a |
| États | ⊥ | 5 | 8 | 7 | 0 |
m - 2…
TestAutomateMiroir pour tester l'automate des suffixes de miroir(u)=bbabab.
analyser, basée sur l'algorithme du miroir, qui prend en argument un texte t et retourne la liste de toutes les positions initiales du mot u=bababb recherché dans le texte t.analyser sur le texte t=babbabaabababbaaabababbbaba.Référence. C. Charras - T. Lecroq : Reverse Factor algorithm